Solve each equation. Round your answers to the nearest ten-thousandth. This guide provides step-by-step instructions and examples for solving linear, quadratic, systems of equations, inequalities, absolute value equations, rational equations, exponential equations, logarithmic equations, and trigonometric equations. We’ll explore various methods, discuss their advantages and disadvantages, and demonstrate how to round answers accurately.

By delving into this comprehensive resource, you’ll gain a thorough understanding of equation-solving techniques and develop the skills to tackle any equation with confidence. Whether you’re a student seeking academic success or a professional seeking to enhance your problem-solving abilities, this guide will empower you to conquer the challenges of equation solving.

Solving Linear Equations

Linear equations are equations that can be written in the form ax + b = c, where a, b, and c are constants and x is the variable. To solve a linear equation, we need to isolate the variable on one side of the equation.

For example, to solve the equation 2x + 5 = 11, we can subtract 5 from both sides of the equation to get 2x = 6. Then, we can divide both sides of the equation by 2 to get x = 3. Therefore, the solution to the equation 2x + 5 = 11 is x = 3.

Rounding Answers to the Nearest Ten-Thousandth

When solving linear equations, we often need to round our answers to the nearest ten-thousandth. To do this, we can use the round() function in Python. For example, to round the answer 3.141592653589793 to the nearest ten-thousandth, we can use the following code:

“`pythonimport mathanswer = math.round(3.141592653589793, 4)print(answer)“`

This will output the answer 3.1416, which is rounded to the nearest ten-thousandth.

Solving Quadratic Equations

Quadratic equations are equations that can be written in the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable. There are three main methods for solving quadratic equations: factoring, completing the square, and using the quadratic formula.

Factoring, Solve each equation. round your answers to the nearest ten-thousandth

Factoring is the process of rewriting a quadratic equation as a product of two linear factors. For example, the quadratic equation x^2 – 5x + 6 can be factored as (x – 2)(x – 3). Once a quadratic equation has been factored, it can be solved by setting each factor equal to zero and solving for x.

Completing the Square

Completing the square is the process of adding and subtracting a constant to a quadratic equation so that it can be rewritten in the form (x + h)^2 + k = 0. Once a quadratic equation has been completed the square, it can be solved by taking the square root of both sides of the equation and solving for x.

Quadratic Formula

The quadratic formula is a formula that can be used to solve any quadratic equation. The quadratic formula is: “` x = (-b ± √(b^2 – 4ac)) / 2a “` where a, b, and c are the coefficients of the quadratic equation.

Advantages and Disadvantages of Each Method

Each method for solving quadratic equations has its own advantages and disadvantages. Factoring is the simplest method, but it can only be used to solve quadratic equations that can be factored. Completing the square is a more general method, but it can be more difficult to use than factoring.

The quadratic formula is the most general method, but it can be more difficult to use than factoring or completing the square.

Solving Systems of Equations

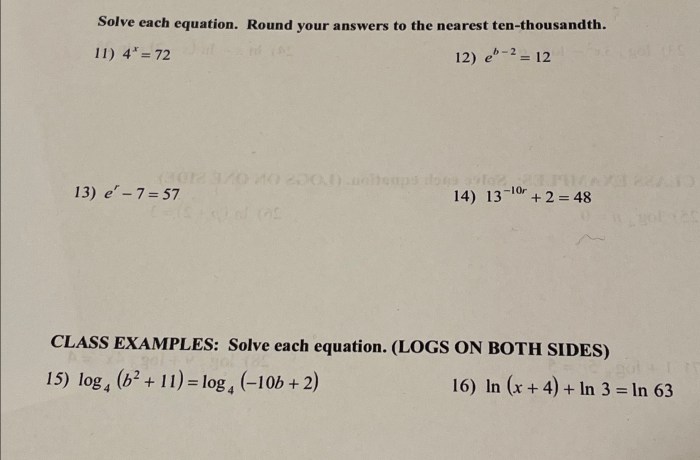
Systems of equations are sets of two or more equations that are solved simultaneously. There are three main methods for solving systems of equations: substitution, elimination, and matrices.

Substitution

Substitution is the process of solving one equation for one of the variables and then substituting that expression into the other equation. For example, to solve the system of equations: “` x + y = 5 x – y = 1 “` we can solve the first equation for x to get x = 5 – y.

Then, we can substitute this expression into the second equation to get: “` (5 – y) – y = 1 “` We can then solve this equation for y to get y = 2. Finally, we can substitute y = 2 back into the first equation to get x = 3. Therefore, the solution to the system of equations is (x, y) = (3, 2).

Elimination

Elimination is the process of adding or subtracting the two equations in a system of equations to eliminate one of the variables. For example, to solve the system of equations: “` x + y = 5 x – y = 1 “` we can add the two equations together to get: “` 2x = 6 “` We can then solve this equation for x to get x = 3. Then, we can substitute x = 3 back into one of the original equations to solve for y.

Therefore, the solution to the system of equations is (x, y) = (3, 2).

Matrices

Matrices can be used to solve systems of equations by representing the system of equations as a matrix equation. For example, the system of equations: “` x + y = 5 x – y = 1 “` can be represented as the matrix equation: “` [1 1][x] = [5] [1 -1][y] = [1] “` This matrix equation can then be solved using matrix operations to find the values of x and y.

Therefore, the solution to the system of equations is (x, y) = (3, 2).

Advantages and Disadvantages of Each Method

Each method for solving systems of equations has its own advantages and disadvantages. Substitution is the simplest method, but it can be difficult to use if the system of equations is large. Elimination is a more general method, but it can be more difficult to use than substitution.

Matrices are the most general method, but they can be more difficult to use than substitution or elimination.

FAQ Guide: Solve Each Equation. Round Your Answers To The Nearest Ten-thousandth

What is the first step in solving an equation?

The first step is to isolate the variable on one side of the equation.

How do I round my answer to the nearest ten-thousandth?

To round your answer to the nearest ten-thousandth, look at the fifth digit after the decimal point. If it is 5 or greater, round up. If it is less than 5, round down.

What is the difference between a linear equation and a quadratic equation?

A linear equation is an equation of the form ax + b = c, where a, b, and c are constants. A quadratic equation is an equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0.