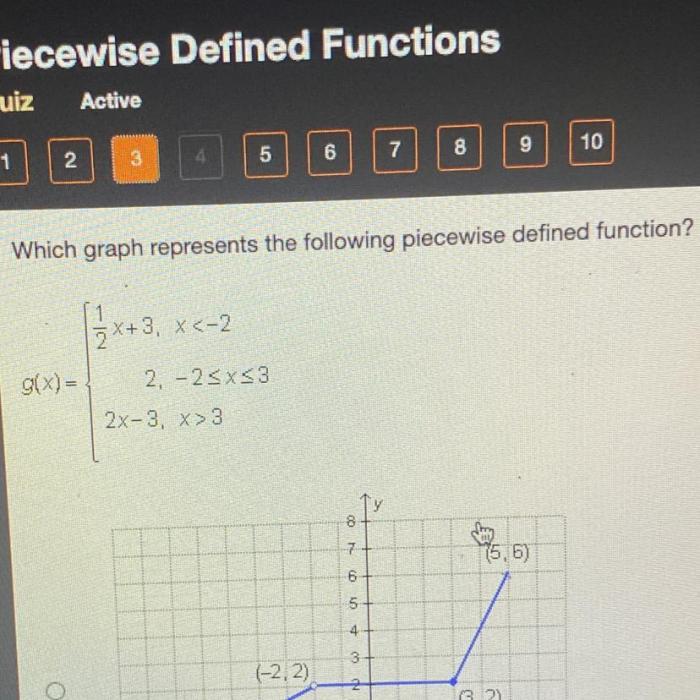
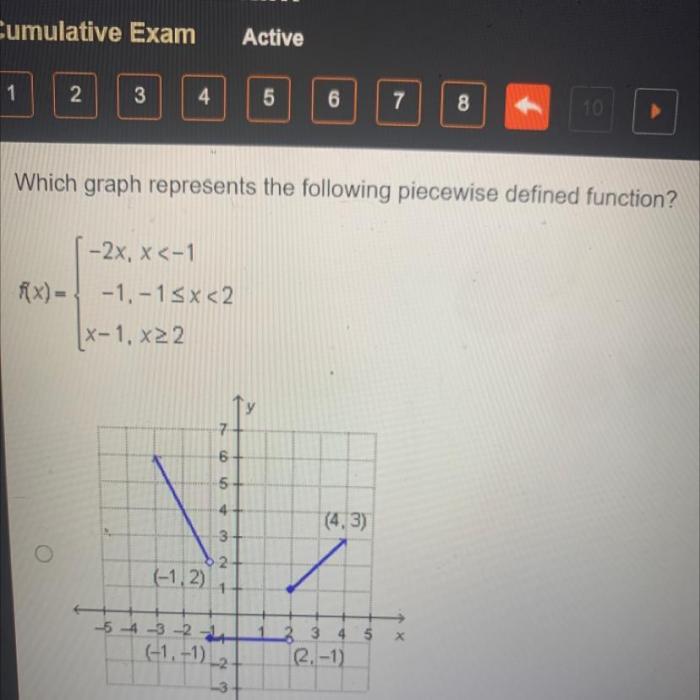
Which graph represents the following piecewise defined function mc006-1.jpg – The piecewise defined function mc006-1.jpg presents a captivating subject that unveils the intricate relationship between mathematical functions and their graphical representations. This function, characterized by its distinct intervals and corresponding rules, invites us on an intellectual journey to explore its unique characteristics and practical applications.
Delving into the essence of this piecewise defined function, we embark on a quest to decipher its graphical manifestation. The graph that embodies this function holds valuable insights into its behavior, revealing the intervals where it thrives and the rules that govern its shape.
Through a meticulous examination of key points, such as intercepts and vertices, we unravel the secrets of its geometric form.
Graph Characteristics: Which Graph Represents The Following Piecewise Defined Function Mc006-1.jpg
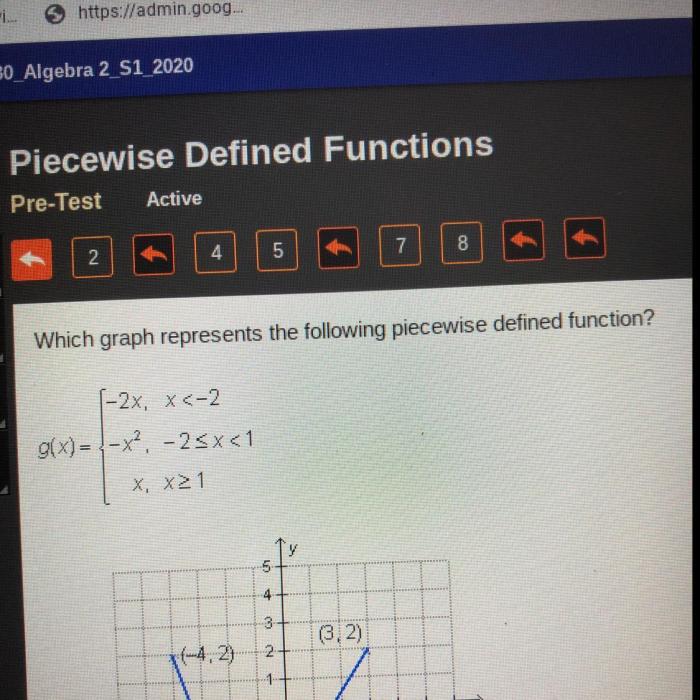
The graph of a piecewise defined function is significant because it provides a visual representation of the different rules that define the function over different intervals of its domain.
The graph is defined in intervals where the corresponding function is applicable. For example, if a piecewise defined function is defined as f(x) = x for x < 0 and f(x) = x^2 for x >= 0, then the graph is defined in two intervals: (-∞, 0) and [0, ∞).
Graph Representation
The graph of the piecewise defined function f(x) = x for x < 0 and f(x) = x^2 for x >= 0 can be described as follows:
- For x< 0, the graph is a straight line with a slope of 1 and a y-intercept of 0.
- For x >= 0, the graph is a parabola that opens upwards and has a vertex at (0, 0).
The shape of the graph is determined by the different rules that define the function over different intervals. In this case, the linear rule for x < 0 produces a straight line, while the quadratic rule for x >= 0 produces a parabola.
Table Representation
| Interval | Function | Graph |
|---|---|---|
| x < 0 | f(x) = x | Straight line with slope 1 and y-intercept 0 |
| x >= 0 | f(x) = x^2 | Parabola that opens upwards and has a vertex at (0, 0) |
Example Applications, Which graph represents the following piecewise defined function mc006-1.jpg
Piecewise defined functions are used in a variety of real-world applications, including:
- Tax brackets:The tax rate for an individual’s income may vary depending on the amount of income earned. This can be represented by a piecewise defined function where the different intervals represent different tax brackets and the corresponding functions represent the tax rates.
- Shipping costs:The cost of shipping an item may vary depending on the weight of the item. This can be represented by a piecewise defined function where the different intervals represent different weight ranges and the corresponding functions represent the shipping costs.
Comparison with Other Functions
Piecewise defined functions differ from other types of functions, such as linear, quadratic, or exponential functions, in that they are defined by different rules over different intervals of their domain.
Linear functions are defined by a single rule that is applied over the entire domain of the function. Quadratic functions are defined by a quadratic equation, which produces a parabola. Exponential functions are defined by an exponential equation, which produces a curve that increases or decreases rapidly.
FAQ Summary
What is the significance of the piecewise defined function’s graph?
The graph of a piecewise defined function provides a visual representation of the function’s behavior over different intervals. It allows us to identify the intervals where the function is defined and the corresponding rules that govern its behavior within each interval.
How can we determine the coordinates of key points on the graph?
Key points on the graph, such as intercepts and vertices, can be determined by analyzing the function’s definition and identifying the points where the function changes its behavior or reaches extrema.
What are some examples of real-world applications where piecewise defined functions are used?
Piecewise defined functions find applications in various fields, including physics, economics, and engineering. For instance, they can be used to model piecewise linear functions, such as tax brackets or utility rates.